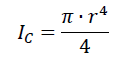GFI130 - Projeto De Física
Experimental I (Turma 33B)
Prof. Dr. José Alberto Nogales
LAVRAS-MG
2021
RESUMO
Este trabalho apresenta um estudo teórico e experimental acerca do fenômeno mecânico de vibração. Tem como objetivo entender e verificar a importância dos principais parâmetros relacionados a esse evento, principalmente referente à frequência natural do sistema. O estudo se baseou na análise teórica e aplicação experimental de algumas réguas de alumínio em vibração livre, em que a captação dos dados experimentais se deu através de uma implementação digital entre o acelerômetro MPU6050, o Arduino e o Matlab. Furos circulares foram feitos nas réguas para fins de comparação dos resultados. Foi constatado que o projeto opera coerentemente com pequenos erros, atestando sua funcionalidade dentro da faixa de frequência (0-20 Hz), e demonstra aplicabilidade no meio acadêmico em experimentos para obter frequência natural de pequenas estruturas.
O objetivo principal do projeto é
construir um protótipo que consiga receber e analisar as vibrações em pequenas estruturas,
visando o melhor custo-benefício possível. Ademais, também se tem como objetivo
verificar a capacidade do equipamento, identificando suas limitações e
precisões. Espera-se que o sistema apresente pequenos erros, atestando sua
funcionalidade dentro de uma pequena faixa de frequência de 0 a 50 Hz para a
análise de vibrações.
Através de alguns experimentos
com uma régua de alumínio, almeja-se a obtenção dos gráficos de análise
dinâmica de vibrações – de Aceleração x Tempo e Magnitude x Frequência - para
comparação com os valores teóricos de vibração natural da régua (frequência
natural). Dados que serão obtidos através do acelerômetro MPU6050, que
apresenta precisão satisfatória para fins educacionais, que é o enfoque deste
projeto.
1.1.1 Conceitos importantes
Qualquer movimento que se repita
após um intervalo de tempo é denominado vibração ou oscilação. O balançar de um
pêndulo e o movimento de uma corda dedilhada são exemplos típicos de vibração
(RAO, 2008). A teoria de vibração trata do estudo e movimentos oscilatórios de
corpos e as forças associadas a eles. Em geral, um sistema vibratório inclui um
meio para armazenar energia potencial (mola ou elasticidade), um meio para
armazenar energia cinética (massa ou inércia) e um meio de perda gradual de
energia (amortecedor).
A vibração de um sistema envolve
a transferência alternada de sua energia potencial para energia cinética e de
energia cinética para energia potencial. Se o sistema for amortecido, certa
quantidade de energia é dissipada em cada ciclo de vibração e deve ser
substituída por uma fonte externa, se for preciso manter um regime permanente
de vibração (RAO, 2008).
De acordo com Rao (2008), as
vibrações podem ser classificadas de várias maneiras, como vibração livre e
forçada, não amortecida e amortecida, linear e não linear, determinística e
aleatória. Como o enfoque deste trabalho será a vibração livre, somente esse
tópico será aprofundado.
· Vibração
livre: “Se um sistema, após uma perturbação inicial, continuar a vibrar por
conta própria, a vibração resultante é conhecida como vibração livre. Nenhuma
força externa age sobre o sistema. A oscilação de um pêndulo simples é um
exemplo de vibração livre” (RAO, 2008, p. 08).
Por outro lado, uma vibração forçada
ocorre se um sistema estiver sujeito a uma força externa (muitas vezes, uma
força repetitiva), e a vibração resultante é conhecida como vibração forçada. A
oscilação que surge em máquinas, como motores a diesel, é um exemplo de
vibração forçada. Se a frequência da força externa coincidir com uma das frequências
naturais do sistema, ocorre uma condição conhecida como ressonância, e o
sistema sofre oscilações perigosamente grandes (RAO, 2008). Falhas de
estruturas como edifícios, pontes, turbinas e asas de aviões foram associadas à
ocorrência de ressonância. Portanto, o entendimento da frequência natural de um
sistema é uma peça-chave para a compreensão deste trabalho.
· Frequência
Natural: “Se, após uma perturbação inicial, um sistema continuar a vibrar por
si próprio sem a ação de forças externas, a frequência com que ele oscila é
conhecida como sua frequência natural” (RAO, 2008, p. 25). Um sistema
vibratório com n graus de liberdade terá, em geral, n frequências
naturais de vibração distintas.
Tendo em vista a importância do
conhecimento da frequência natural em um sistema mecânico, os procedimentos
experimentais utilizados para a análise de vibrações visam em sua maioria a
obtenção dessa frequência natural do sistema. Em geral, a resposta de um
sistema vibratório depende das condições iniciais, bem como das excitações
externas. Um sistema vibratório é um sistema dinâmico para o qual as variáveis
como as excitações (entradas) e respostas (saídas) são dependentes do tempo. Por
serem dependentes do tempo (Diagrama Aceleração x Tempo, por exemplo), são
utilizadas técnicas computacionais para que a resposta do sistema seja dada no
domínio da frequência. Essa transformação do tempo para a frequência pode ser
feita através da transformada rápida de Fourier (FFT – Fast Fourier
Transform).
· Transformada rápida de Fourier: A FFT recebe sinais analógicos de tensão que podem ser referentes a deslocamento, velocidade, aceleração, deformação ou força em relação ao tempo. O sinal é convertido para digital e é transformado em frequência. Essa mudança é dada por transformações matemáticas da série de Fourier, daí vem a denominação.
·Função resposta em frequência (FRF): A FRF pode ser usada para determinar a resposta de um sistema a qualquer tipo de força excitadora no domínio da frequência. O analógico é enviado pelo acelerômetro, ou transdutores de forças, para o analisador de espectro.
As várias quantidades encontradas na área da vibração e do som (como deslocamento, velocidade, aceleração, pressão e força) são frequentemente representadas usando a notação de Decibel, que pode ser expresso como:
onde X0 é uma tensão de referência especificada. Na prática, a equação anterior é usada para expressar as razões entre quantidades como deslocamentos, velocidade, acelerações e pressões. De modo geral, o valor de referência X0 para a aceleração é considerado como 1 ug = 9,81 x 10-6 m/s² (RAO, 2008).
1.1.2 Modelo teórico
Tendo em vista a análise de vibrações proposta neste trabalho, que será realizada em uma régua de alumínio presa em uma de suas extremidades em uma mesa, o seguinte modelo teórico que trata sobre uma viga se faz jus à experimentação proposta.
A equação do movimento do
sistema para essas condições (viga sujeita à vibração livre), como demonstrado
por RAO (2008), é a seguinte:
onde E é o módulo de rigidez do material da viga (Módulo de
Young), I é o momento de inércia da seção transversal, Y(x) ou f(x) é o
deslocamento na direção y em função de x da extremidade fixa (Figura 01), ω é a
frequência natural circular e m é a massa por unidade de comprimento, sendo
representado por “m = ρ.A(x)”, em que ρ é a densidade do material e x é
a distância medida a partir da extremidade fixa.
Figura 01 – Representação do problema.
Fonte: Rao (2008).
Seguindo algumas operações
matemáticas e obedecendo às seguintes condições iniciais (viga engastada):
Obtém-se a fórmula final para
cálculo das frequências naturais da viga, ao se resolver a equação diferencial
(2), como é demonstrado por Rao (2008):
onde ωn é a enésima frequência natural ([ωnf] = rad/s), L ou l é a distância do engaste até a extremidade da viga e αn é uma constante que pode assumir diferentes valores para o cálculo das diversas frequências naturais do sistema. Para o caso do projeto em questão, somente αn = 1,875 é interessante, pois se trata do primeiro modo de vibração da régua e corresponde à menor frequência natural, que é a frequência natural fundamental do sistema.
O momento de inércia I da seção
transversal pode ser calculado, para uma viga maciça, utilizando os valores da
largura, b, e da espessura, h, através da seguinte equação (HIBBELER, 2009):
Caso
haja um furo na viga, o momento de inércia será alterado. Para fins de
simplificação nos cálculos, considerando que o furo realizado na viga é bem
pequeno em relação ao tamanho total da estrutura, pode-se considerar que o
centroide, o centro geométrico da viga/régua, se mantém o mesmo da régua
maciça. Dessa forma, através do Teorema dos Eixos Paralelos, como é bem
definido por Hibbeler (2009), o novo momento de inércia quando a estrutura
apresenta um furo circular, é o seguinte:
Onde
IC é o momento de inércia do furo circular em relação ao eixo que
passa pelo centroide do furo, A é a área do furo e d a distância entre o
eixo do furo e o centroide da régua, que de acordo com as considerações
anteriores, se mantém o mesmo da régua maciça ao considerar que o furo seja bem
pequeno. O momento de inércia IC do furo circular pode ser calculado
da seguinte maneira (HIBBELER, 2009), sabendo-se que r é o raio do furo:
2 MATERIAIS UTILIZADOS E PROCEDIMENTO EXPERIMENTAL
O projeto se consistiu na implementação digital entre o
sensor de vibração MPU6050, o Arduino e o Matlab para tratamento dos dados. As
primeiras semanas do desenvolvimento do projeto se basearam na otimização dos
códigos que foram utilizados na configuração do Arduino e do Matlab para a
coleta dos dados – códigos demonstrados no Anexo I. Assim, a seguir é descrito
todos os materiais utilizados.
· Sensor MPU6050
O sensor MPU6050 possui um acelerômetro, um giroscópio, um sensor de temperatura e um processamento interno para a realização de cálculos com o intuito de tratar os dados obtidos pelo sensor, aliviando o processamento do Arduino, neste caso. O sensor possui também duas entradas auxiliares para a junção com outro sensor, sendo o processamento interno compatível com alguns tipos de sensores, realizando um tratamento desses dados. O MPU6050 é conectado ao Arduino via conexão I2C.
Fonte: Dos autores (2021).
O acelerômetro é um dispositivo usado para medir a
aceleração própria de um sistema. O princípio básico de funcionamento por trás dele
é o sistema de massa e mola. As molas, enquanto dentro da sua região linear,
são governadas pela lei de Hooke. Outro princípio físico envolvido é a segunda
lei de Newton, que relaciona força com massa e aceleração. Igualando as duas
equações obtém-se “ma=kx” e, portanto, pode-se perceber que uma
aceleração a causa um deslocamento da massa de “x=(ma)/k”, ou,
alternativamente, se a massa sofre um deslocamento x, significa que a
massa está sob uma aceleração de “a=(kx)/m” (RAO, 2008). Acelerômetros,
tipicamente, convertem energia mecânica em um sinal elétrico mensurável.
Geralmente a saída é expressa em milivolts, de modo que a sensibilidade é dada
em mV por g. Os acelerômetros são oferecidos em uma ampla gama de
sensibilidades e a sensibilidade ideal depende do nível do sinal a ser medido.
Na prática, para sinais de baixa amplitude, costuma-se usar dispositivos de
alta sensibilidade. Para sinais de grande amplitude, usa-se acelerômetros de
sensibilidade menor. A sensibilidade pode, ainda, variar com a frequência da
aceleração a ser medida.
O dispositivo em questão, sensor MPU6050, não apresenta
uma precisão tão concisa, mas é satisfatória para fins educacionais, que é o
enfoque deste projeto.
Para implementar o sensor junto
ao arduino, foi-se necessário também utilizar ferro de solda e cabos jumpers.
·
Arduino
Arduino é uma plataforma de prototipagem eletrônica de
hardware livre e de placa única, projetada com um microcontrolador Atmel AVR
com suporte de entrada/saída embutido, uma linguagem de programação padrão. O
arduino utilizado foi o Arduino Uno.
Figura 03 – Arduino UNO utilizado.
Fonte: Dos autores (2021).
· Réguas
de alumínio
O experimento teve como objetivo
obter as frequências naturais de uma régua de alumínio em 3 diferentes
situações: régua maciça, régua com um furo na extremidade e régua com um furo
no meio. Todos os furos realizados nas réguas foram de 0,2cm de diâmetro e,
apesar de algumas imperfeições, foram considerados circulares. A seguinte
Figura 04 ilustra os três diferentes casos.
Figura 04 – Réguas utilizadas no experimento.
Fonte: Dos autores (2021).
Para o procedimento experimental
de coleta de dados, é fixada a régua de alumínio com o auxílio de fitas
adesivas, em uma mesa reta e fixa. A régua deve estar fixada de forma que
esteja firme, mas tenha espaço suficiente sobrando para poder oscilar quando provocada.
Na parte da régua que está
fixada na mesa, o sensor de vibrações deve ser estabilizado, com o auxílio de
fita adesiva, vide Figura 05. A partir disso, foram causadas vibrações através
da aplicação de uma força na vertical, simplesmente para tirar a régua do
repouso, como está ilustrado na Figura 01. Vibrações essas que foram computadas
pelo sensor e enviadas através do Arduino para o Matlab, onde foram estudadas.
A distância l utilizada na equação (3) foi de 15cm para todos os
ensaios.
Figura 05 – Experimento sendo realizado.
Fonte: Dos autores (2021).
Após a realização de todas as
etapas descritas acima, furos foram feitos nas réguas utilizando as ferramentas
adequadas. Inicialmente foi feito um furo no centro da régua, e posteriormente,
em outra régua foi feito um furo na sua extremidade, para que seja estudada a implicação
da alteração do momento de inércia da estrutura em sua frequência natural de
oscilação – Equação (3). O sensor foi novamente colocado, e suas alterações
analisadas.
A montagem do circuito foi realizada de acordo com a configuração da Figura 06.

Fonte: Dos autores (2021).
(b)
No software do Arduino IDE é
utilizada a biblioteca Wire para que seja feita a comunicação I2C com o MPU6050.
É então estabelecida comunicação e acessado os registros do sensor para que ele
esteja na função de administração de energia correta e os parâmetros de
sensibilidade dos sensores sejam estabelecidos. O código utilizado está
presente no Anexo I.
Já para o
Matlab, foi criada uma função auxiliadora, a função “diagramas”, que é
responsável por analisar os dados, que tem como entrada dois vetores, um vetor
de aceleração e um de tempo. Ela é responsável por aplicar a FFT (Fast Fourier
Transform), que é uma função que transforma Tempo em Frequência, para que possa
ser plotado os gráficos aceleração (g) tempo (s), magnitude frequência (Hz) e
LogMagnitude frequência (Hz). Os códigos do Matlab também estão presentes no
Anexo I.
A partir dos gráficos e dos picos
de frequência obtidos pode-se observar as frequências naturais do corpo.
3 RESULTADOS
No caso deste experimento em
particular, realizado com uma régua feita de alumínio com dimensões de 3 cm de
largura e 0,1 cm de espessura, tem-se um valor de 7030×106 kg/m²
para o módulo de Young (módulo de rigidez) baseado na consideração de que sua
composição é exclusivamente alumínio (CALLISTER, 2002). Outros dados
importantes são: a densidade do alumínio, 2,7 g/cm³ ou 2700 kg/m³, e o momento
de inércia do material.
No primeiro caso da régua maciça utilizada
neste experimento, calculou-se o momento de inércia com a equação (4),
obtendo-se um resultado de 2,5x10-12 m4.
Para os outros dois casos da
régua com furo, utilizou-se as equações (5) e (6) para realização dos cálculos.
Na régua com um furo no meio, a distância d entre o eixo do furo e o
centroide da régua é nula (passam pelo mesmo eixo), em que o momento de inércia
total será somente o da seção transversal subtraído do momento de inércia do
furo ( I = IT – IC).
Já no caso do furo que foi feito
na extremidade da régua, a distância d entre o centroide do furo e o
centroide total da régua foi de 13,8 cm - equação (5). Obs.: como explicitado
anteriormente, está sendo considerado que o centroide da régua total não se
alterou com a inserção dos furos, uma vez que eles possuem diâmetro de 0,2cm,
sendo muito pequenos.
Assim,
aplicou-se os dados na equação (3) e os seguintes valores teóricos apresentados
na Tabela 01 foram encontrados. Na tabela também estão presentes os valores
experimentais, que similarmente serão detalhados logo em seguida.
Tabela 01 - Resultados teóricos e experimentais obtidos
através dos cálculos das frequências naturais das réguas.
|
Régua |
Momentos de Inércia (m4) |
Valores de Frequência Natural (Hz) |
|
|
- |
- |
Teórico |
Experimental |
|
Normal (maciça) |
2,5000 x 10-12 |
11,58 |
9,93 |
|
Com furo no meio |
1,7146 x 10-12 |
9,59 |
6,79 |
|
Com furo na extremidade |
0,8930 x 10-12 |
6,92 |
5,38 |
A seguir estão também apresentados os gráficos obtidos pelo Matlab, indicando a frequência natural de vibração experimental das réguas, resultantes da análise dos dados coletados pelo sensor MPU6050.
Figura
07 – Gráficos obtidos para a régua normal
sem furos (maciça).

Fonte: Dos autores (2021).
Figura
08 – Gráficos obtidos para a régua com um
furo no meio.
Fonte: Dos autores (2021).
Figura
09 – Gráficos obtidos para a régua com um
furo na extremidade.

Fonte: Dos autores (2021).
O primeiro gráfico dentre os
conjuntos apresentados explicita a aceleração em função do tempo. A aceleração,
no primeiro conjunto de gráficos da régua maciça, está indicada em função da
aceleração da gravidade, ou seja, o valor 0 significa que o valor da aceleração
da gravidade (de aproximadamente 9,78m/s² para o local onde foi realizado) é o
valor de referência. Nos outros conjuntos de gráficos para os outros casos da
régua, optou-se por não aplicar o valor da aceleração da gravidade como
referência, como é possível observar nos gráficos de Aceleração x Tempo das
Figuras 08 e 09, que ao decorrer do tempo, tendem ao valor da aceleração da
gravidade.
Já o segundo gráfico mostra
magnitude por frequência. É neste que se pode tirar a informação da frequência
natural, de forma que esta possui uma magnitude bem elevada em relação às
outras frequências oriundas de ruídos externos e vibrações indesejadas. Estas
magnitudes menores são mais facilmente observadas nos terceiros gráficos de
cada conjunto (LogMagnitude vs frequência), que foi calculado através do Matlab
utilizando a equação (1) apresentada anteriormente.
Os valores analisados estão
representados no eixo Z devido à oscilação propriamente no eixo Z. Dessa forma,
para este experimento, os outros eixos não são relevantes, porém a necessidade
varia para cada sistema vibracional analisado.
4 ANÁLISES E CONCLUSÕES
Analisando
a equação (3) que foi a base do cálculo das frequências naturais teóricas,
percebe-se que o momento de inércia é proporcional ao valor da frequência
natural – ao aumentar o momento de inércia do sistema analisado, a respectiva
frequência natural consequentemente aumentará da mesma forma. Essa
característica foi um fato nos experimentos realizados, uma vez que ao fazer os
furos na régua, o que diminuiu o momento de inércia, os valores de frequência
natural encontrados foram proporcionalmente menores, comprovando esse conceito
teórico.
Apesar
dessa semelhança, observa-se que ocorreram diferenças entre os valores teóricos
e experimentais. Tais diferenças podem ser atribuídas a inúmeros fatores, que
serão listados por conseguinte, começando pelo tipo da régua que fora escolhida
para realização do experimento. A régua ideal para fazer o experimento seria
uma com a seção transversal uniforme, completamente quadrada, e com um material
com um alto módulo de elasticidade (módulo de Young), como um aço comum, por
exemplo. Por ser alumínio, material que possui um índice que representa um
terço do módulo de elasticidade do aço, essa propriedade de elasticidade dá ao
alumínio a vantagem de dar às estruturas uma elevada capacidade de amortecer
golpes e reduzir as tensões produzidas pela variação da temperatura (CALLISTER,
2002). Isso é uma desvantagem para os objetivos deste experimento, uma vez que
o propósito inicial era fazer com que as réguas vibrem, mas, com o material
sendo de alumínio, percebe-se que os ciclos de vibração captados pelo
acelerômetro não ultrapassam 2 segundos ao analisar os gráficos. Isso ocorre em
função do amortecimento que o alumínio exerce sobre a vibração por apresentar
um pequeno módulo de elasticidade quando comparado com outros metais.
Além disso, a régua não possuía
uma seção transversal quadrada, o que pode da mesma forma causar diferenças
entre o modelo teórico adotado e o experimental, uma vez que, para fins de
simplificação, fora considerado que a régua possuía a seção transversal
quadrada. Devido a todos esses fatores, optou-se por adotar a simplificação no
centroide da régua como mencionado anteriormente, pois senão seria necessário
adotar métodos computacionais para realizar o cálculo do momento de inércia, tornando
complexa a análise cuja não é o objetivo deste trabalho. Ademais, como o ciclo
de vibração foi muito pequeno, de menos de 2 segundos, o sensor MPU6050 também
teve alguns problemas de precisão na captação dos dados de aceleração e tempo,
havendo a necessidade de o experimento ser realizado diversas vezes.
Dessa forma, baseado na comparação dos dados obtidos entre os métodos teóricos e experimentais testados e os resultados de diversos testes, é possível afirmar que o sistema opera coerentemente com pequenos erros, atestando sua funcionalidade dentro da faixa de frequência (0-20 Hz). Tudo isso, claro, levando em consideração os fatores explicitados no parágrafo anterior, relativos à régua e ao sensor utilizado. Isso assegura o cumprimento do objetivo inicial do projeto, uma vez que, a um baixo custo, demonstra aplicabilidade no meio acadêmico em experimentos para obter frequência natural de pequenas estruturas tal como os feitos neste trabalho.
Vídeo que sintetiza o trabalho:
BIBLIOGRAFIA
CALLISTER, W. D. Jr. Ciência e Engenharia de Materiais: uma Introdução. LTC, 5ª ed. Rio de Janeiro, RJ, 2002.
ELETROGATE. Acelerômetros MPU-6050, MMA8452 e MPU-9250. Blog. 2020. Disponível em: https://blog.eletrogate.com/acelerometros-mpu-6050-mma8452-e-mpu-9250/. Acesso em: 06 de maio de 2021.
HIBBELER, R. C., Resistência dos Materiais. Pearson Prentice Hall, 7ª edição, São Paulo, 2009.
RAO, S. Vibrações Mecânicas. Pearson Prentice Hall, 4ª ed. São Paulo, SP, 2008.
RODRIGUES, Rogério de Oliveira. Análise dinâmica bidimensional não-linear física e geométrica de treliças de aço e pórticos de concreto armado. 1997. Tese (Doutorado em Estruturas) - Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, 1997. doi:10.11606/T.18.2018.tde-21032018-090933. Acesso em: 2021-04-27.
ANEXO I
Códigos utilizados nos softwares Arduino IDE e Matlab.
Arduino IDE:
#include <Adafruit_MPU6050.h>
#include
<Adafruit_Sensor.h>
#include
<Wire.h>
Adafruit_MPU6050
mpu;
void
setup(void) {
Serial.begin(115200);
while (!Serial) {
delay(10); // vai
pausar Zero até que o console serial abra
}
// Tentando inicializar!!
if (!mpu.begin()) {
Serial.println("Falhou em encontrar o chip do MPU6050");
while (1) {
delay(10);
}
}
mpu.setAccelerometerRange(MPU6050_RANGE_16_G);
mpu.setGyroRange(MPU6050_RANGE_250_DEG);
mpu.setFilterBandwidth(MPU6050_BAND_21_HZ);
Serial.println("");
delay(100);
}
void loop() {
/* Obter novos
eventos do sensor com as leituras */
sensors_event_t a, g, temp;
mpu.getEvent(&a, &g, &temp);
/* Imprimir na tela os valores captados
*/
Serial.print(a.acceleration.x);
Serial.print(",");
Serial.print(a.acceleration.y);
Serial.print(",");
Serial.print(a.acceleration.z);
Serial.print(", ");
Serial.print(g.gyro.x);
Serial.print(",");
Serial.print(g.gyro.y);
Serial.print(",");
Serial.print(g.gyro.z);
Serial.println("");
delay(10);
}
Matlab:
projeto.m
clear all;
clc;
close all;
xyzt=[
-0.280
0.790 9.010 0.000;
-0.310
0.780 8.960 0.040;
-0.400
0.700 8.860 0.040;
-0.450
0.730 8.840 0.040;
-0.490
0.780 8.810 0.080;
-0.500
0.830 8.900 0.080;
-6.260
0.770 9.350 0.080;
11.170
2.140 4.340 0.120;
-9.820
0.380 14.770 0.130;
5.260
1.520 14.410 0.160;
-0.900
0.990 13.210 0.170;
-3.950
0.390 7.440 0.180;
7.470
1.420 4.030 0.200;
-7.780
-0.130 9.070 0.210;
5.080
1.510 12.010 0.220;
-0.110
0.790 10.250 0.240;
-1.720
0.760 8.430 0.250;
4.750
1.190 6.090 0.260;
-4.710
0.290 10.360 0.280;
3.620
1.170 10.760 0.290;
0.600
0.650 9.030 0.320;
-2.800
0.490 8.140 0.330;
3.650
1.160 7.350 0.340;
-2.820
0.630 10.300 0.360;
1.390
1.060 9.640 0.370;
1.280
0.900 8.280 0.380;
-2.480
0.650 8.350 0.400;
2.350
1.200 9.060 0.410;
-1.360
0.770 9.850 0.440;
0.270
0.930 9.280 0.450;
1.890
1.040 8.050 0.460;
-2.030
0.670 8.880 0.480;
1.470
1.030 9.450 0.490;
-0.220
0.840 9.300 0.480;
-0.600
0.890 9.030 0.520;
1.650
1.020 8.510 0.520;
-1.200
0.770 9.380 0.520;
0.550
0.960 9.240 0.560;
0.900
0.920 8.640 0.560;
-0.940
0.740 8.920 0.600;
1.140
0.950 9.020 0.600;
-0.030
0.860 9.250 0.600;
-0.120
0.890 9.070 0.640;
0.980
0.930 8.690 0.640;
-0.790
0.780 9.090 0.640;
0.660
0.950 9.170 0.680;
0.420
0.960 8.900 0.680;
-0.450
0.910 8.940 0.720;
0.730
1.040 8.870 0.720;
-0.450
0.910 9.130 0.720;
0.070
0.970 9.070 0.760;
0.500
0.990 8.870 0.760;
-0.560
0.890 9.020 0.760;
0.470
0.970 9.070 0.800;
0.070
0.890 9.100 0.800;
-0.140
0.900 9.080 0.800;
0.470
0.950 8.970 0.840;
-0.440
0.910 9.040 0.840;
0.120
0.990 9.070 0.880;
0.220
0.960 8.940 0.880;
-0.430
0.890 9.000 0.880;
0.290
0.980 8.990 0.920;
-0.130
0.960 9.050 0.920;
-0.130
0.930 8.980 0.920;
0.260
0.970 8.980 0.960;
-0.320
0.900 9.040 0.960;
0.120
0.940 9.070 0.960;
0.050
0.940 9.010 1.000;
-0.310
0.940 9.000 1.000;
0.150
1.020 8.980 1.040;
-0.240
0.970 9.030 1.040;
-0.180
0.950 9.020 1.040;
0.060
0.990 8.980 1.080;
-0.380
0.930 9.020 1.080;
0.000
0.980 9.020 1.080;
-0.100
0.960 8.970 1.120;
-0.280
0.960 9.000 1.120;
0.060
0.980 9.030 1.120;
-0.230
0.940 9.000 1.160;
]
figure('Name','Eixo X')
diagramas(xyzt(:,4),xyzt(:,1))
figure('Name','Eixo Y')
diagramas(xyzt(:,4),xyzt(:,2))
figure('Name','Eixo Z')
diagramas(xyzt(:,4),xyzt(:,3))
diagramas.m
function diagramas(tempo, magnitude)
X_mags=abs(fft(magnitude))
Fs=1/(tempo(2)-tempo(1))
N=length(magnitude)
bin_vals=(0:N-1)
fax_Hz= bin_vals*Fs/N
N_2= ceil(N/2)
subplot(3,1,1)
plot (tempo,magnitude)
title ('Aceleração vs Tempo')
subplot(3,1,2)
plot(fax_Hz(2:N_2),X_mags(2:N_2))
title ('Magnitude vs Frequencia')
axis tight
subplot (3,1,3)
plot(fax_Hz(2:N_2),20*log10(X_mags(2:N_2)))
title ('Magnitude (LOG) vs Frequencia')
axis tight